圆柱作为几何学中的基本形体之一，具有广泛的应用领域，为了更好地掌握圆柱的相关知识，本文将围绕圆柱专题进行系统的复习，帮助读者深入理解圆柱的性质、公式及应用。

圆柱的基本性质

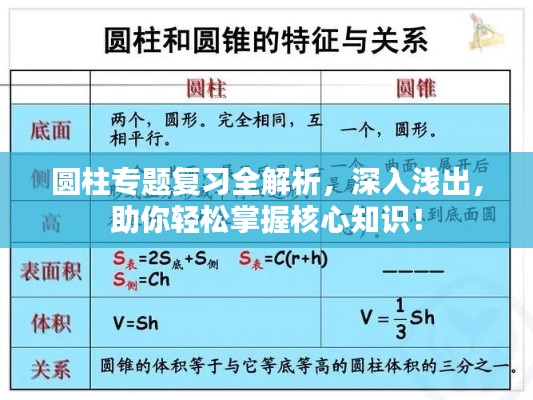
1、定义：圆柱是由平面上的圆绕其直径旋转一周所生成的立体。

2、构成要素：底面为圆，侧面为曲面，有两个底面相互平行且相等。

3、性质：圆柱的底面半径、高、母线等参数决定了其体积和表面积。

圆柱的体积与表面积

1、体积公式：V = πr²h，其中r为底面半径，h为高。

2、表面积公式：S = 2πr² + 2πrh，其中r为底面半径，h为高，表面积包括两个底面的圆面积和侧面的面积。

圆柱的应用

1、实际应用：圆柱在建筑工程、机械制作、艺术品制作等领域有广泛的应用。

2、练习题：通过解决一系列与圆柱相关的实际问题，加深对圆柱知识的理解与运用。

圆柱的专题复习方法

1、梳理知识：回顾圆柱的基本性质、体积公式、表面积公式等基础知识。

2、练习题目：通过做大量的练习题，加深对圆柱知识的理解与运用。

3、总结归纳：对练习过程中出现的错误进行反思，总结归纳解题方法和思路。

4、拓展延伸：了解圆柱在各个领域的应用，拓宽视野，提高解决问题的能力。

常见题型及解题方法

1、已知条件求参数：已知圆柱的底面半径和高，求其体积和表面积；已知圆柱的表面积，求其底面半径和高等，通过设立方程，求解未知数。

2、图形组合问题：涉及圆柱与其他几何形体的组合，需分析组合图形的性质，求解相关问题。

3、实际应用题：涉及圆柱在生活中的实际应用，如建筑、机械等领域，需将实际问题抽象为数学模型，然后求解。

复习注意事项

1、掌握基础知识：熟练掌握圆柱的基本性质、体积公式、表面积公式等基础知识。

2、加强练习：通过大量的练习，加深对圆柱知识的理解与运用。

3、注意单位换算：在解决实际问题时，注意单位换算，确保结果的准确性。

4、培养空间想象力：通过想象和理解三维图形，提高空间想象力，有助于解决复杂的几何问题。

本文通过对圆柱专题的复习，系统地总结了圆柱的基本性质、体积与表面积的公式、应用及解题方法，希望读者能够认真复习，熟练掌握圆柱的相关知识，提高解决几何问题的能力。